追加記事あり:2018は7から18までの連続した整数の自乗和らしいので、似たような現象がこの先いつあるか調べてみた-完全版
元旦ですね。
今年は僕が喪中なので新年のご挨拶はありません。
Twitterでおもしろい投稿が流れてきた。
以下のとおり。
【2018の特徴】
①偶数
②約数は4つ
③2つの素数の2乗和
④12連続整数の2乗和
特に④の「12連続整数の2乗和」になる数は珍しく、同じような性質を持っている1つ前の数は1730、1つ後の数は2330です。このような数の年が次に来るのは300年以上後になります。
https://twitter.com/naganomath/status/947237346826625024
とのこと。
今年2018年は7から18の自乗和らしい。
しかし、「12連続整数の2乗和」を待たずとも、13連続とか14連続とかならもっと直近にあるのでは?とも思った。
そこで、似たような現象がこの先いつあるか調べてみた。
以下、計算に使ったマクロ。
Sub CalcJijyowa()
Dim cTate As Long
Dim cYoko As Long
For cTate = 1 To 8
Range("A1").Offset(cTate).Value = cTate
Next
For cYoko = 12 To 19
Range("A1").Offset(, cYoko - 11).Value = cYoko
Next
Dim cSum As Long
Dim cNum As Long
Dim cTgt As Long
For cNum = 8 To 8 + 12 - 1
cSum = cSum + cNum ^ 2
Next
cTgt = cSum
Dim cList As Long
cList = 2
For cTate = 1 To 8
For cYoko = 12 To 19
cSum = 0
For cNum = cTate To cTate + cYoko - 1
cSum = cSum + cNum ^ 2
Next
Range("A1").Offset(cTate, cYoko - 11).Value = cSum
If cSum >= 2018 And cSum <= cTgt Then
Range("A1").Offset(cTate, cYoko - 11).Font.Color = vbRed
Range("A1").Offset(cTate, cYoko - 11).Font.Bold = True
Range("L" & cList).Value = cTate & "から"
Range("M" & cList).Value = cYoko & "個連続"
Range("N" & cList).Value = cSum
cList = cList + 1
End If
If cSum >= cTgt Then
Exit For
End If
Next
Next
Range("L1").Value = "最初の数字"
Range("M1").Value = "自乗回数"
Range("N1").Value = "合計値"
Range("L1").CurrentRegion.Sort Key1:=Range("N1"), Order1:=xlAscending, Header:=xlYes
For cNum = 2 To cList - 1
Debug.Print Range("L" & cNum).Value & " " & Range("M" & cNum).Value & " : " & Range("N" & cNum).Value
Next
End Sub
以下は、出力結果。
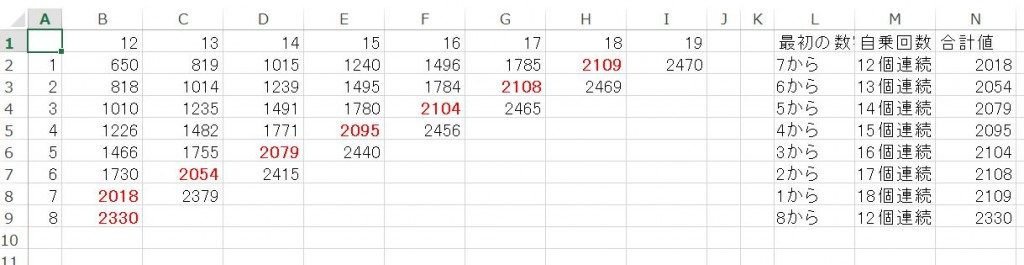
2018は7から連続した12個の数値の自乗和らしいので、似たような現象がこの先いつあるか調べてみた。その結果。
7から 12個連続 : 2018 ←今年
6から 13個連続 : 2054 ←この次
5から 14個連続 : 2079 ←さらにその次
4から 15個連続 : 2095 ←以下つづく…。
3から 16個連続 : 2104
2から 17個連続 : 2108
1から 18個連続 : 2109
8から 12個連続 : 2330
300年待たないでも、直近81年の間にもっと数値が連続するイベントが目白押し…とまでは言わないが、いろいろあるようだ。
もっと書きたいのだけど、これから天皇杯の横浜マリノス-セレッソ大阪戦を観に行かなくてはなので、これにて。
追加記事あり:2018は7から18までの連続した整数の自乗和らしいので、似たような現象がこの先いつあるか調べてみた-完全版
今気がついたのだけど、むしろ、少ない数の連続した自乗和になることのほうが価値が高いのか。。あとでやりなおしだ orz。